Vetor definido por dois pontos
Nem sempre um vetor é representado por um segmento que parte da origem do sistema. Consideremos o vetor \(\overrightarrow{AB}\) de origem no ponto \(A(x_{1}, y_{1})\) e extremidade em \(B(x_{2}, y{2})\).
Os vetores \(\overrightarrow{OA}\) e \(\overrightarrow{OB}\) possuem as expressões analíticas:
\(\overrightarrow{OA}= (x_{1}, y_{1})\) e \(\overrightarrow{OB} = (x_{2}, y_{2})\).
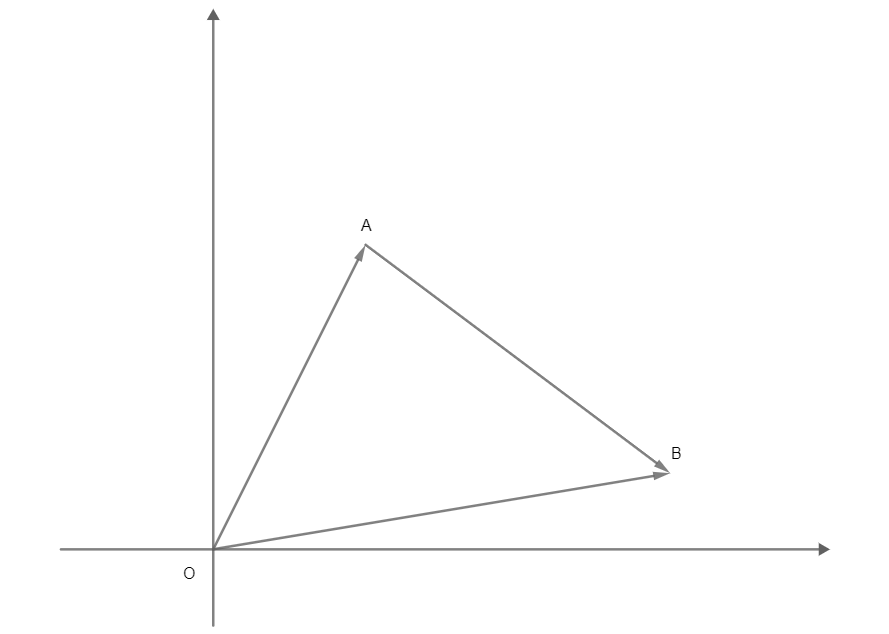
Do triângulo OAB da figura acima, temos que:
\(\overrightarrow{OA} + \overrightarrow{AB} = \overrightarrow{OB}\)
Isolando \(\overrightarrow{AB}\),
\(\overrightarrow{AB} = \overrightarrow{OB} – \overrightarrow{OA}\).
Como \(\overrightarrow{OA}= (x_{1}, y_{1})\) e \(\overrightarrow{OB} = (x_{2}, y_{2})\), temos que:
\(\overrightarrow{AB} = (x_{2}, y_{2}) – (x_{1}, y_{1})\)
Assim,
\(\overrightarrow{AB} = (x_{2}, x_{1},\; y_{2} – y_{1})\)
Ou seja, as componentes de \(\overrightarrow{AB}\) são obtidas fazendo \(B – A\)
\(\overrightarrow{AB} = B – A\)
Referências:
STEINBRUCH, Alfredo. Geometria Analítica . 1ª ed. Pearson Universidades, 1995.
Was this helpful?
0 / 0