Potencial elétrico de uma carga puntiforme

Potencial elétrico de uma carga puntiforme

Vamos considerar uma carga puntiforme \(Q\), geradora de um campo elétrico, e uma carga de prova \(q\), posicionada em um ponto \(P\) desse campo elétrico, a uma distância \(d\) da carga geradora.

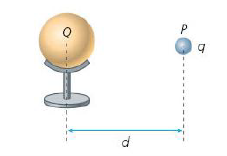
A carga de prova \(q\), ao ser colacada em \(P\), adquire energia potencial \(E_{\text {pel }}\).

A energia potencial elétrica \(E_{\text {pel }}\) do sistema constituído por \(Q\) e q é dada por:

$$ E_{p e l}=k \cdot \frac{Q q}{d} $$

A dedução dessa expressão envolve conhecimentos mais avançados de Matemática. Por isso, vamos adotá-la sem demonstrar.

Nessa expressão, \(k\) é a constante eletrostática do meio, para a qual temos no vácuo o seu maior valor: \(k=k_0=9 \cdot 10^9 \mathrm{~N} \cdot \mathrm{m}^2 / \mathrm{C}^2\).

Essa energia é também a energia potencial elétrica da carga \(Q\) ou a energia potencial elétrica da carga \(q\).

Mas, conforme vimos no início deste capítulo, a energia potencial elétrica, \(E_{\mathrm{pe}}\), adquirida por uma carga de prova q, ao ser posicionada no campo elétrico, é dada por: \(E_{\text {pel }}=q V\).

Assim, podemos escrever que:

$$ q V=k \cdot \frac{Q q}{d} \Rightarrow V=k \cdot \frac{Q}{d} $$

Pelo fato de o potencial elétrico ser uma grandeza escalar, uma carga elétrica positiva gera potencial elétrico positivo e uma carga elétrica negativa gera potencial elétrico negativo.

Observações:

– Observe na figura 4 que uma linha de força do campo elétrico é sempre orientada no sentido dos potenciais decrescentes.

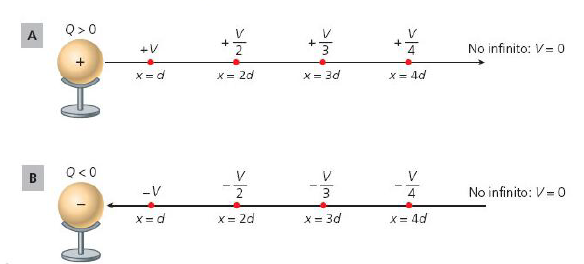
O potencial elétrico sempre diminui ao se percorrer uma linha de força ao longo de sua orientação.

– Uma superfície na qual todos os pontos têm um mesmo potencial elétrico é denominada superfície equipotencial.

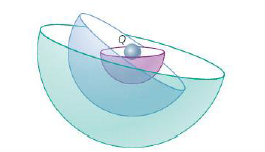
Para uma carga elétrica puntiforme \(Q\) as superfícies equipotenciais são superfícies concêntricas na carga.

– As linhas de força do campo elétrico são perpendiculares às superfícies equipotenciais.

Linhas de força e as superfícies equipotenciais no campo elétrico (A) de uma carga puntiforme e (B) no campo elétrico uniforme.

– As fórmulas apresentadas para a energia potencial e o potencial elétrico são válidas para um ponto de referência infinitamente afastado. Nesse ponto, a energia potencial e o potencial elétrico são nulos.