Leis de Ohm
A partir de dados obtidos experimentalmente, o professor e físico alemão Georg Simon Ohm verificou em 1826 uma propriedade que se tornou conhecida como primeira lei de Ohm.
A diferença de potencial \(U\) nos terminais de um resistor mantido a temperatura constante e percorrido por uma corrente elétrica de intensidade ié diretamente proporcional à intensidade dessa corrente.
Assim, nas condições das experiências de \(\mathrm{Ohm}\), quando se aumenta a ddp \(U\) aplicada aos terminais de um resistor, a intensidade \(i\) de corrente elétrica que o atravessa aumenta na mesma proporção. Portanto, a resistência elétrica \(R\) do resistor permanece constante.
Matematicamente, escrevemos:
$$ \frac{U_1}{i_1}=\frac{U_2}{i_2}=\frac{U_3}{i_3}=\ldots=\frac{U_n}{i_n}=\text { constante }=R $$
Portanto, de acordo com a primeira lei de Ohm, temos: \(U=R i\)
Os resistores cuja resistência elétrica é constante são denominados resistores ôhmicos.
O diagrama \(U \times i\) de um dado componente de circuito elétrico é denominado curva característica.
Para os diversos tipos de resistores, temos as curvas características mostradas na figura abaixo.
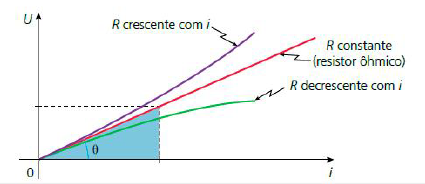
Para um resistor ôhmico, vale a relaçāo:
$$ R \stackrel{N}{=} \operatorname{tg} \theta $$
Como vimos, para calcular a potência de um bipolo elétrico, fazemos: \(P=U i\) Podemos, então, combinar essa expressão com a relação \(U=R i\).
– Se \(U=R i\), então: \(P=U i \Rightarrow P=(R i) i \Rightarrow P=R i^2\)
– Se \(U=R i \Rightarrow i=\frac{U}{R}\), então: \(P=U i \Rightarrow P=U \cdot \frac{U}{R} \Rightarrow P=\frac{U^2}{R}\)
Observação:
As duas relações obtidas para o cálculo da potência aplicam-se apenas a resistores.
A partir de dados obtidos em experimentos realizados com condutores fabricados artesanalmente, Ohm verificou uma propriedade que se tornou conhecida como segunda lei de Ohm.
A resistência elétrica de um condutor homogêneo de seção transversal constante depende do material do qual ele é feito, é diretamente proporcional ao seu comprimento \(L\) e inversamente proporcional à área \(S\) da sua seção transversal.
Consideremos o condutor mostrado na figura abaixo.
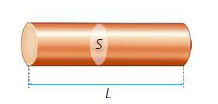
A resistência de um condutor depende de suas características geométricas.
Matematicamente, podemos escrever: \(R=\rho \cdot \frac{L}{S}\)
O coeficiente de proporcionalidade representado pela letra grega \(\rho\) (lê-se: rô) é denominada resistividade elétrica. A resistividade elétrica é uma característica do material do qual é feito o condutor e depende de sua temperatura. No SI, a resistividade é medida em \(\Omega \cdot \mathrm{m}\).
Referências:
Ferraro, Nicolau Gilberto Física, volume único / Nicolau Gilberto Ferraro, Carlos Magno A. Torres, Paulo Cesar M. Penteado. 1. ed. – São Paulo: Moderna, 2012. – (Vereda digital)
Was this helpful?
0 / 0