Quando uma função é par?
Uma função \(f: A \to B\) é par se, e somente se, f(a) = f(-a) para qualquer \(a \in A\).
Por exemplo:
Observe o gráfico da função \(f\left(x\right) = x^{2}\)
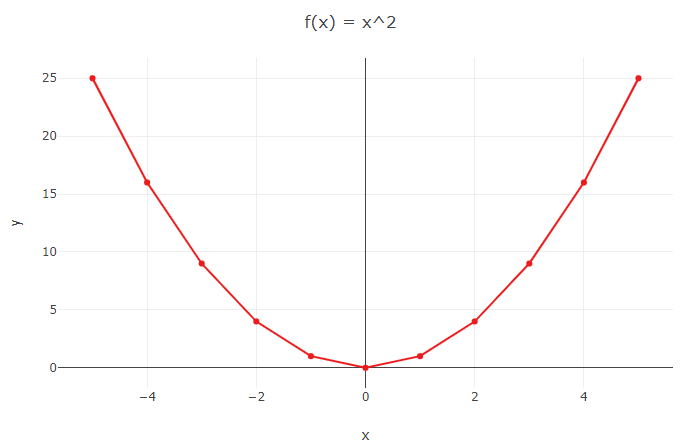
A função \(f\left(x\right) = x^{2}\) é par pois, \(f\left(a\right) = a^{2}\) e \(f\left(-a\right) = \left(-a\right)^{2}\). Ou seja, \(f\left(a\right) = f\left(-a\right), \forall a \in R\)
Antecedentes simétricos implicam em imagens iguais.
Observe que se uma função f é par e \(\left(a, b\right) \in f \) então \(\left(-a, b\right) \in f\). Como \(\left(a, b\right)\) e \(\left(-a, b\right)\) são pontos simétricos em relação ao eixo y (ordenadas) podemos concluir que toda função par tem como representação gráfica uma curva simétrica em relação ao eixo das ordenadas (0y).
Função impar
Quando uma função é impar?
Uma função \(f: A \to B\) é impar se, e somente se, f(a) = -f(-a) para qualquer \(a \in A\).
Observe o gráfico da função \(f\left(x\right) = x^{3}\) abaixo.
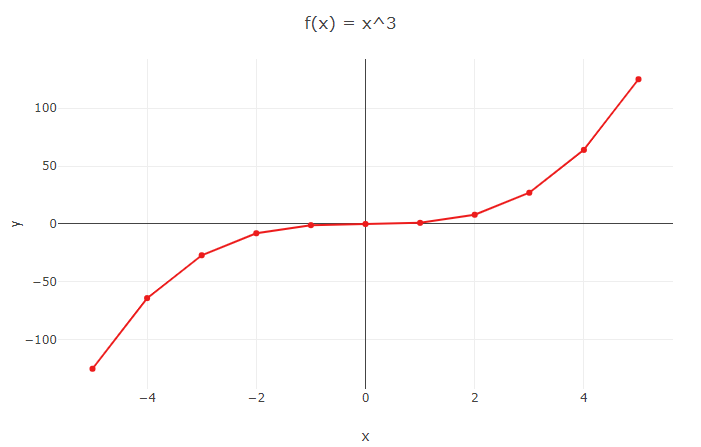
A função R \(f(x) = x^{3} é ímpar pois, \(f\left(a\right) = a^{3}\) e \(f\left(-a\right) = \left(-a\right)^{3}\). Ou seja, \(f\left(a\right) = -f\left(-a\right), \forall a \in R\)
Antecedentes simétricos implicam em imagens iguais.
Em resumo:
Função par \(\Leftrightarrow \) \(f\left(a\right) = f\left(-a\right), \forall a \in D_{f}\)
Função impar \(\Leftrightarrow \) \(f\left(a\right) = f-\left(-a\right), \forall a \in D_{f}\)
Referências:
Aranha, Álvaro Zimmermann. Funções e logaritmos/Álvaro, Zimmermann Aranha, Manoel Benedito Rodrigues. -2.ed. rev. melhor. – São Paulo: Policarpo. 1994 – (Exercícios de matemática; v.2).
Was this helpful?
0 / 0