Pontos no plano cartesiano
Essa ideia foi criada pelo filósofo e matemático francês René Descartes (1596-1650), em um trabalho publicado em 1637. Ele mostrou que usando como referência um par de retas que se interceptavam, era possível construir um sistema no qual números poderiam estar associados a pontos.
O ponto O representa a intersecção entre as duas retas, o ponto P tem uma distância horizontal de 3 unidades e uma distancia vertical de 2 unidades. E para indicar a posição do ponto P, usamos o par de números (5, 4). O ponto O é indicado pelo par de números (0, 0).

Essa representação recebeu o nome de plano ou sistema cartesiano.
Como usar um plano cartesiano?
Primeiramente, este é apenas um exemplo das diversas aplicações do plano cartesiano. Vamos supor que o esquema abaixo representa uma cidade. Três amigos, Ana, Pedro e Toninho, combinaram de se encontrar no centro da Praça dos Perdidos. Ana é indicada pela letra A, Pedro é indicado pela letra P e Toninho é indicado pela letra T. Tomando como referência o centro da Praça dos Perdidos, podemos dizer que:

- Ana esta a 8 quadras a direita e 3 quadras acima do centro da Praça dos perdidos.
- Pedro esta a 4 quadras a direita e 1 quadra acima da Praça dos Perdidos.
- Toninho esta 5 quadras a direita e 2 quadras acima da Praça dos Perdidos.
Agora vamos aos passos para criar o plano cartesiano representando esse esquema:
1° Passo: Traçamos duas retas perpendiculares, a horizontal chamamos de eixo x, e a vertical chamamos de eixo y.
2° Passo: Identificamos os pontos de intersecção entre as duas retas, como tomamos a Praça dos Perdidos como ponto de referência então este será a nossa origem (0, 0).
3° Passo: Usando segmentos de mesma medida, associamos o lado de cada quadra a esse segmento. Usaremos números naturais para identificar as quadras situadas à direita e acima do centro da praça.
Sendo assim:
Ana esta na posição (8, 3)
Pedro esta na posição (4, 1)
Toninho esta na posição (5, 2)
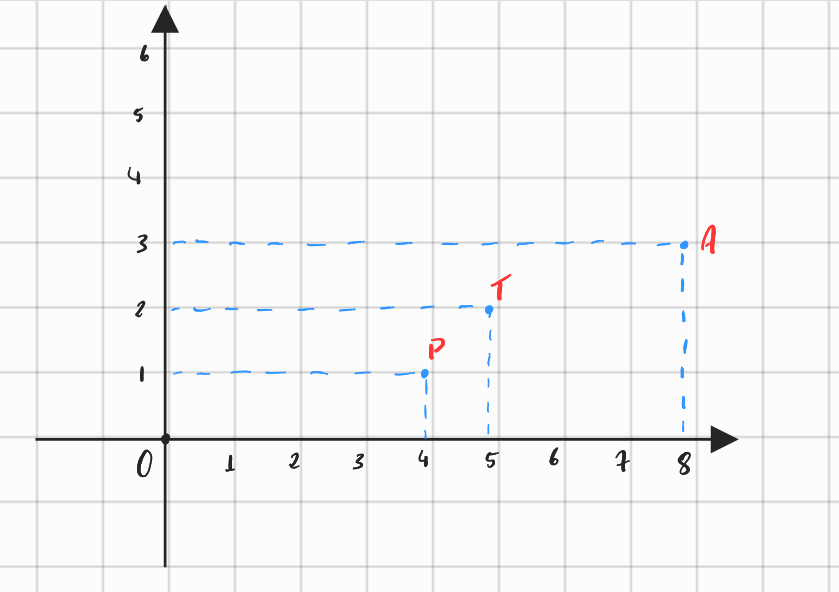
Esses pares de números são chamados de pares ordenados, porque por convenção escrevemos primeiro lugar o número do eixo x e, em seguida, o número do eixo y.
Com base no que foi feito acima vamos observar como se constrói um sistema de coordenadas cartesianas:
- traçamos duas retas perpendiculares: uma horizontal, chamada eixo x, e outra vertical, chamada eixo y;
- o ponto de intersecção dos dois eixos recebe o nome de origem do sistema e corresponde ao par ordenado (0, 0);
- nos eixos, a cada ponto fazemos corresponder um número natural.

Um sistema assim recebe o nome de plano cartesiano.
Assim todo ponto fica definido a partir de dois valores: um no eixo x e outro no eixo y, ou seja, um par ordenado (x, y) que é chamado de coordenadas do ponto.
Como construir polígonos no plano cartesiano?
Já vimos que o encontro entre duas arestas determina um vértice e que os vértices são pontos. E acabamos de aprender a associar pontos ao plano cartesiano.
Com esses conhecimentos podemos usar o plano cartesiano para representar polígonos, posicionando seus vértices usando coordenadas no plano e com isso podemos extrair informações desse polígono através das coordenadas do vértice.
Vamos começar construindo um quadrado usando um plano cartesiano.
Primeiro escolhemos um ponto qualquer no plano para marcar o primeiro vértice.

Agora escolhemos o comprimento do lado do quadrado, lembrando que o quadrado tem quatro lados iguais, marcamos os outros três vértices.

Por ultimo traçamos as arestas, finalizando a construção do nosso quadrado.

Agora vamos observar as coordenadas dos vértices desse quadrado desenhado:
A(3, 2)
B(3, 6)
C(7, 6)
D(7, 2)
Como o quadrado possui os quatro lados iguais sabemos que:
$$ \operatorname{med}(\overline{\mathrm{AB}})=\operatorname{med}(\overline{\mathrm{BC}})=\operatorname{med}(\overline{\mathrm{CD}})=\operatorname{med}(\overline{\mathrm{DA}})=4 \text { u.c. } $$
Observe que ao subtrair os valores referentes ao eixo x obtemos o comprimento do segmento definido por esses pontos. De forma similar obtemos o comprimento dos segmentos na vertical subtraindo os valores referentes ao eixo y.
Referências
Giovanni Júnior, José Ruy A conquista da matemática: 6o ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018.
Was this helpful?
1 / 0