Sistema de numeração decimal
Sistema de numeração decimal
O nosso sistema de numeração nasceu em uma região conhecida como vale do rio Indo, atual Paquistão. Usando grupos de dez, os hindus desenvolveram um sistema de numeração que estabelecia a ideia de posição. Nesse sistema, eram usados símbolos diferentes para representar as quantidades de 1 a 9 símbolo para o zero foi criado pelos hindus no século VI e, inicialmente, era representado por um ponto ou por um pequeno círculo. A partir do século VIII, os árabes passaram a adotar o Sistema de Numeração Hindu, por ser prático e facilitar os cálculos. Quando povoaram o norte da África e parte da Espanha, os árabes ocidentais introduziram os símbolos hindus, que deram origem aos símbolos que conhecemos hoje, os símbolos indo-arábicos, e ao sistema de numeração conhecido como Sistema de Numeração Decimal, utilizado até hoje. A denominação indo-arábico deve-se ao fato de os símbolos e as regras que regem esse sistema terem sido criados pelos hindus e aperfeiçoados e divulgados pelos árabes. Os símbolos indo-arábicos também são conhecidos como algarismos. Veja o porquê: o matemático Mohammed ibn Musa al-Khwarizmi (780-850), autor do primeiro livro árabe conhecido com explicações detalhadas sobre os cálculos hindus, ganhou tanta reputação nos países da Europa Ocidental que o seu nome se tornou sinônimo dos símbolos inventados pelos hindus. Assim, a palavra algarismo tem origem no nome al-Khwarizmi.
As transformações dos símbolos indo-arábicos
Os algarismos indo-arábicos sofreram várias transformações na sua representação antes de adquirirem, no século XVI, a aparência que conservam até hoje.
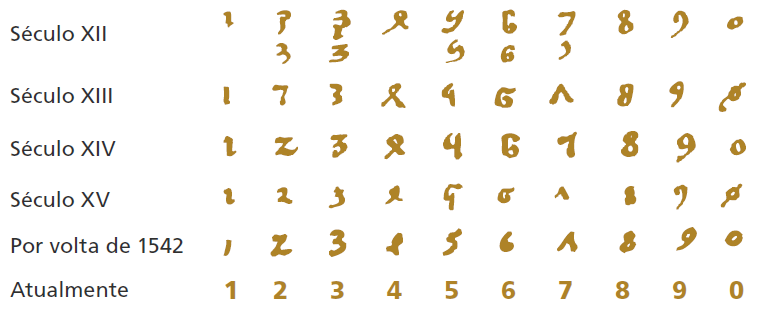
O zero: uma invenção importante
Os primeiros que chegaram à noção de zero foram os babilônios, povo que habitou a Mesopotâmia, atual Iraque, por volta de 2500 a.C. Na América Central, os maias também chegaram à representação do zero e usavam várias formas para representá-lo. Os indianos conheciam a noção de vazio e empregavam a palavra shúnya para representá-lo. Os árabes chamavam o zero de shfr. Já na
Europa, levado pelos árabes, ficou conhecido como zephirum, depois zéfiro, zefro e, finalmente, zero. Dos indianos aos árabes, a forma do zero mudou de um ponto para um círculo. Na Europa, o zero encontrou forte resistência. Várias superstições e o medo do desconhecido impediam o seu uso. Além disso, com a popularização do conhecimento do zero e dos outros algarismos indo-arábicos, havia o perigo de que qualquer um pudesse fazer contas, habilidade que, até então, poucos detinham.
Um costume muito antigo!
Você já observou que o nosso sistema de numeração é decimal, isto é, contamos sempre em grupos de dez? Esse costume vem, sobretudo, do fato de o ser humano ter aprendido a contar usando os dedos das mãos.
A palavra “decimal” é de origem latina, decem, que significa dez. É por esse motivo que o nosso sistema de numeração é chamado de Sistema de Numeração Decimal.
A sequência dos números naturais
Iniciando pelo zero e acrescentando sempre uma unidade, teremos a sequência dos números naturais:
$$ 0,1,2,3,4,5,6,7,8,9,10,11,12, \ldots $$
Os números naturais constituem um conjunto numérico denominado conjunto dos números naturais, que se indica pela letra \(\mathrm{N}\) :
$$ N=\{0,1,2,3,4,5,6,7,8, \ldots\} $$
Quando se exclui o zero do conjunto \(\mathbf{N}\), temos o conjunto dos números naturais não nulos, indicado por \(\mathrm{N}^*\) :
$$ N^*=\{1,2,3,4,5,6,7, \ldots\} $$
Essa sequência numérica é utilizada no cotidiano para fazermos contagens, por exemplo, dos dias do mês, da quantidade de alunos em uma sala de aula, entre outros.
Características importantes do nosso sistema de numeração
– Com apenas estes dez símbolos, pode-se escrever qualquer número natural, por maior que seja:
1 2 3 4 5 6 7 8 9 0
Esses símbolos são os algarismos indo-arábicos.
– O sistema decimal é de base 10, já que os agrupamentos sao feitos de dez em dez.
– O sistema decimal é posicional, porque, dependendo da posiçao que ocupa no número, o mesmo símbolo pode representar valores diferentes.
Exemplo: 323 tem o algarismo 3 com valor posicional trezentos (300) e valor posicional três (3).
$$ \begin{array}{r} 323 \\ 4 \\ 3003 \end{array} $$
– O sistema indo-arábico utiliza o zero para indicar uma “casa vazia” dentre os agrupamentos de dez do número considerado.
Exemplos: 205, 100, \(1023 .\)
– O sistema decimal é multiplicativo, porque um algarismo escrito à esquerda de outro vale dez vezes o valor posicional que teria se estivesse ocupando a posição desse outro. Exemplo:
777 = 700 + 70 + 7 = 7 x 100 + 7×10 + 7×1
A reta numérica
Para representar a sequência dos números naturais, utilizamos a reta numérica. Trata-se de um importante instrumento para comparar e ordenar números. Então, vamos construir uma reta numérica em seu caderno:
1º) Utilizando uma régua, trace uma reta em uma folha em branco; em seguida, marque um ponto em qualquer parte da reta e marque o número zero nesse ponto (a numeração terá início nesse ponto).
2°) Marque outro ponto à direita do zero para representar o número 1. Utilize a régua novamente para medir a distância entre o zero e o 1.
3°) Em seguida, encontre a posição exata do número 2 na reta: utilizando a régua, marque o número 2 medindo a mesma distância que você obteve no passo anterior.
4°) Repita o passo anterior para os números 3, 4, 5, 6, 7, 8, 9, 10, 11, …, até o número que você quiser.
5°) Finalmente desenhe duas pontas de seta, uma antes do zero e outra após o último número de sua reta numérica.

Pronto, agora temos uma reta numérica que serve de base para representação de números naturais.
Comparar e ordenar números naturais
Ao comparar dois números naturais distintos, utilizamos os símbolos > (maior que) e < (menor que). Podemos usar a reta numérica para fazermos a comparação. Para isso, precisamos lembrar que os números da reta numérica estão em ordem crescente e que todo número à direita de outro número sempre será maior. Por exemplo: o número 4 está localizado à direita do número 3 e à esquerda do número 5. Então, vamos comparar os números 3, 4 e 5 utilizando a reta numérica. Podemos afirmar que:

4 > 3 Lê-se: quatro é maior que três.
4 < 5 Lê-se: quatro é menor que cinco.
Em ordem crescente, podemos afirmar que 3 < 4 < 5.
O valor posicional
Escreva o número 675, troque de lugar os algarismos 7 e 5 e obtive 657.
O número que escrevi primeiro é maior ou menor que o número que obtive?
Antes da troca: quanto valia o 5 no primeiro número?
Depois da troca: quanto passou a valer o 5?
Agora, veja este outro número: 7 056
Que troca eu devo fazer para o 6 aumentar seu valor em 100 vezes? Que número eu
obtenho nesse caso?
Que troca eu devo fazer para o 6 aumentar seu valor em 10 vezes? Que número eu
obtenho nesse caso?
Você observou que o valor do algarismo depende da posição que ele ocupa no número?
No número 26, o valor do algarismo 2 é 2 x 10, ou seja, 20 unidades, porque ele ocupa a posição ou a ordem das dezenas.
No número 263, o valor do algarismo 2 é 2 x 100, ou seja, 200 unidades, porque ele ocupa a posição ou a ordem das centenas. Vamos considerar o número 8 594.
Escrevemos o número 8 594 por extenso e o lemos assim: oito mil, quinhentos e noventa e quatro. Veja o quadro de ordens até a 10a ordem:
| 10ª ordem | 9ª ordem | 8ª ordem | 7ª ordem | 6ª ordem | 5ª ordem | 4ª ordem | 3ª ordem | 2ª ordem | 1ª ordem |
| Unidades de bilhão | Centenas de milhão | Dezenas de milhão | Unidades de milhão | Centenas de milhar | Dezenas de milhar | Unidades de milhar | Centenas de unidade simples | Dezenas de unidade simples | Unidades simples |
Este quadro pode ser simplificado para que você possa localizar a ordem dos números que deseja.
| Unidades de bilhão | Centenas de milhão | Dezenas de milhão | Unidades de milhão | Centenas de milhar | Dezenas de milhar | Unidades de milhar | Centenas de unidade simples | Dezenas de unidade simples | Unidades simples |
Lendo e escrevendo um número natural
No Sistema de Numeração Decimal, os números são lidos ou escritos mais facilmente quando separamos os algarismos em grupos de três, começando pela direita. Isso porque cada três ordens forma uma classe. Veja os números: 6 283 104 640 e 5 000 254.
| Centenas de bilhão | Dezenas de bilhão | Unidades de bilhão | Centenas de milhão | Dezenas de milhão | Unidades de milhão | Centenas de milhar | Dezenas de milhar | Unidades de milhar | Centenas de unidade simples | Dezenas de unidade simples | Unidades simples |
| 6 | 2 | 8 | 3 | 1 | 0 | 4 | 6 | 4 | 0 |
| Centenas de bilhão | Dezenas de bilhão | Unidades de bilhão | Centenas de milhão | Dezenas de milhão | Unidades de milhão | Centenas de milhar | Dezenas de milhar | Unidades de milhar | Centenas de unidade simples | Dezenas de unidade simples | Unidades simples |
| 5 | 0 | 0 | 0 | 2 | 5 | 4 |
Cada grupo de três algarismos constitui uma classe, e cada classe tem um nome, como podemos ver a seguir.
Classe das unidades simples (1ª classe)
Nessa classe temos as unidades simples, dezenas de unidades simples, centenas de unidades simples.
Classe dos milhares (2ª classe)
Nessa classe temos as unidades de milhar, as dezenas de milhar e as centenas de milhar.
Classe dos milhões (3ª classe)
Nessa classe temos as unidades de milhão, dezenas de milhão e centenas de milhão.
Classe dos bilhões (4ª classe)
Nessa classe temos as unidades de bilhão, dezenas de bilhão e centenas de bilhão.

Quando todas as ordens de uma classe são representadas por zero, não se lê essa classe. Lemos ou escrevemos por extenso: cinco milhões, duzentos e cinquenta e quatro.
Referências
Giovanni Júnior, José Ruy A conquista da matemática: 6o ano: ensino fundamental: anos finais / José Ruy Giovanni Júnior, Benedicto Castrucci. — 4. ed. — São Paulo: FTD, 2018.