Potencial elétrico no campo elétrico uniforme
Em posts anteriores, estudamos o campo elétrico uniforme gerado, por exemplo, por duas placas planas paralelas e eletrizadas com cargas de mesmo módulo, porém de sinais opostos.
Vamos considerar, então, uma carga de prova \(q\), positiva, abandonada em um ponto \(A\) de um campo elétrico uniforme, de módulo \(E\), que se desloca até \(B\). A figura abaixo mostra a situação descrita e as duas superfícies equipotenciais, \(S_{\mathrm{A}}\) e \(S_{\mathrm{B}}\), de potenciais elétricos \(V_A\) e \(V_B\), que passam por \(A\) e \(B\).
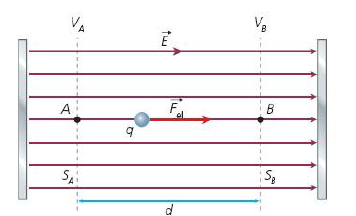
Na carga elétrica (q), a força elétrica tem módulo constante, pois o campo elétrico é uniforme.
Já vimos que o trabalho da força elétrica, em qualquer deslocamento entre dois pontos de um campo elétrico, pode ser calculado fazendo:
$$ \tau_{\mathrm{Fel}_{\mathrm{el}}}=q \cdot\left(V_A-V_B\right) $$
Sendo \(V_A-V_B=U\), temos:
$$ \tau_{F_{e l}}=q U \text { (1) } $$
Entretanto, no caso particular de o campo elétrico ser uniforme, a força elétrica será constante em módulo, direção e sentido; assim, o trabalho poderá ser calculado por: \(\tau_{\mathrm{Fel}}=\mathrm{Fel}{\mathrm{el}} d \cdot \cos \theta\) A força elétrica tem a mesma direção e o mesmo sentido do deslocamento \((\theta=) (0^{\circ}) \), e sendo \(F{\mathrm{el}}=q E\) podemos escrever que:
$$ \tau_{F_{\mathrm{el}}}=F d \Rightarrow \tau_{F_{\mathrm{el}}}=q E d $$
Comparando(2) e (1), obtemos:
$$ q E d=q U \Rightarrow E d=U $$
Observações:
- Nessa expressão, U é tomada em valor absoluto.
- De \(E d=U\) e \(F=q E\), concluímos que: \(E=\frac{U}{d}=\frac{F}{q}\)
Em unidades do SI, temos \(1 \frac{\text { volt }}{\text { metro }}=1 \frac{\text { newton }}{\text { coulomb }} \Rightarrow 1 \frac{\mathrm{V}}{\mathrm{m}}=1 \frac{\mathrm{N}}{\mathrm{C}}\)
No SI, a unidade oficial de medida de intensidade do vetor campo elétrico é \(\frac{V}{m}\)
Referências:
Ferraro, Nicolau Gilberto Física, volume único / Nicolau Gilberto Ferraro, Carlos Magno A. Torres, Paulo Cesar M. Penteado. 1. ed. – São Paulo: Moderna, 2012. – (Vereda digital)
Was this helpful?
0 / 0