Energia potencial gravitacional
Energia potencial gravitacional
Responda de acordo com o texto.
- O que é energia potencial gravitacional?
- O que ocorre quando você solta um objeto de uma determinada altura?
Energia potencial gravitacional é a energia mecânica associada ao trabalho da força peso.
Se soltarmos uma bola de certa altura \(h\) acima do solo e desprezarmos a resistência do ar, ela cairá, adquirindo energia cinética durante a queda. Como não é possível criar nem destruir energia, concluímos que a energia cinética adquirida pela bola durante sua queda já estava “armazenada” em sua posição inicial. A essa energia, momentaneamente armazenada numa posição inicial, devido à interação entre a Terra e o corpo, damos o nome de energia potencial gravitacional ( \(E_{\text {pgrav }}\) ). Dizemos que a energia potencial gravitacional inicial da bola foi gradativamente convertida em energia cinética durante sua queda. Considerando nula a energia potencial gravitacional no solo, ao fim da queda a energia cinética final da bola tem valor igual ao de sua energia potencial gravitacional inicial.
Se invertermos a situação, isto é, se lançarmos a bola do solo para o alto com a mesma energia cinética com a qual ela chegou após a queda, ela atingirá a mesma altura \(h\) da primeira experiência.
O valor da energia potencial gravitacional é calculado em relação a um nível horizontal de referência, em geral o solo, no qual adotamos \(E_{\mathrm{Pgrav}}=0\).
A figura abaixo mostra a energia potencial gravitacional de um corpo no solo, adotado como nível zero de energia potencial gravitacional, e a uma altura \(h\) acima do solo.
Acima do nível de referência, a energia potencial gravitacional é positiva:
\(E_{\text {pgrav }}=+m g h\)

Abaixo do nível de referência, a energia potencial gravitacional é negativa:
$$ E_{\text {pgrav }}=-m g h $$
Você, sentado em sua cadeira assistindo às aulas, tem energia potencial gravitacional positiva em relação ao chão da sala, pois está acima dele. Porém, em relação ao teto dessa mesma sala, sua energia potencial gravitacional é negativa, pois você está abaixo dele.
Energia potencial gravitacional positiva significa que o corpo pode, espontaneamente, chegar ao nível zero de energia potencial (o corpo pode cair). Energia potencial gravitacional negativa significa que o corpo não pode, espontaneamente, chegar ao nível zero de energia potencial; para chegar ao nível zero é necessária a realização de um trabalho. Existem outros tipos de energias potenciais, que podem ser tanto positivas como negativas, falaremos mais sobre elas em outras aulas, pode verificar na playlist do canal.
Resumindo, podemos calcular a energia potencial gravitacional em relação a qualquer plano horizontal de referência, no qual adotamos \(E_{\mathrm{pgrav}}=0\). Acima desse plano, o corpo tem energia potencial gravitacional positiva: \(E_{\text {pgrav }}=+m g h\). Abaixo desse plano, o corpo tem energia potencial gravitacional negativa:
\(E_{\text {pgrav }}=-m g h\).
A tabela abaixo mostra a energia potencial gravitacional de três bolas, para três níveis de referência diferentes.
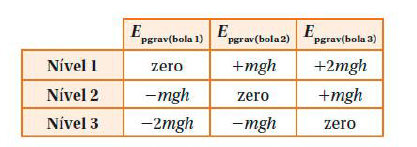

Observe que, para uma mesma bola, a energia potencial gravitacional varia de acordo com o nível de referência considerado. No entanto, a diferença dos valores entre dois níveis quaisquer é sempre a mesma, isto é, a energia potencial gravitacional no nível 2 é sempre \(m g h\) acima da energia potencial gravitacional no nível 1. A energia potencial gravitacional no nível 1 é sempre \(+m g h\) acima da energia potencial gravitacional no nível 2 e sempre \(+2 m g h\) acima da energia potencial gravitacional no nível \(3 .\)
Observe também que, quando deslocamos o corpo entre dois níveis quaisquer, a diferença entre os valores inicial e final da energia potencial gravitacional é exatamente igual ao trabalho da força peso nesse deslocamento. Veja os exemplos:
I. Uma bola vai do nível 2 para o nível 1, que é tomado como referência.
\(E_{\text {pgrav(2) }}-E_{\text {pgrav }(1)}=+m g h-0=+m g h=\tau_{\vec{p}(2>1)}\)
II. Uma bola vai do nível 1 , que é tomado como referência, para o nível 3.
\(E_{\mathrm{pgrav}(1)}-E_{\mathrm{pgrav}(3)}=0-(+2 m g h)=-2 m g h=\tau_{\vec{p}(1 \rightarrow 3)}\)
Portanto, para a força peso \((\vec{P})\) são sempre verdadeiras as igualdades:
$$ \begin{gathered} \tau_p=-\Delta E_{\mathrm{pgrav}} \\ \text { ou } \\ \tau_p=E_{\mathrm{pgrav(inicial})}-E_{\mathrm{pgrav}(\text { final })} \end{gathered} $$
Referências:
Ferraro, Nicolau Gilberto Física, volume único / Nicolau Gilberto Ferraro, Carlos Magno A. Torres, Paulo Cesar M. Penteado. 1. ed. – São Paulo: Moderna, 2012. – (Vereda digital)
Tag:Energia, Física, Gravitacional, Potencial