Currículo em ação – Respostas, Caderno do Aluno – 1 Ano do Ensino Médio 3 bimestre.
Aulas 7 e 8 – Resolução de Equações Utilizando Fatoração
1. Utilizando estratégias de fatoração, determine as raízes das equações:
a. \(3 x^{2}+15 x=0\)
b. \(x^{2}+16 x=0\)
c. \((x-3)(x+6)=0\)
d. \(x^{2}+2 x-35=0\)
e. \(x^{2}-6 x+5=0\)
Resposta:
a) \(3 x^{2}+15 x=0\)
Colando o fator comum em evidência \(x(3 x+15)=0\) fazemos \(x=0\) ou
\(3 x+15=0\)
\(3 x=-15\)
\(x=-5\).
Logo, as raízes da equação são \(s={0,-5} \).
b. \(x^{2}+16 x=0\)
\(x^{2}+16 x=0=\) colando 0 fator comum om evidência \(x(x+16)=0=\) fazemos \(x=0\) ou \(x+16=0\) segue que \(x=-16 \), sendo assim, as raízes da equação são \(S=\{0,-16\}\).
c. \((x-3)(x+6)=0\)
Como a equação já esta fatorada podemos seguir com:
i) \(x-3=0\) logo \(x=3\)
ii) \(x+6=0\) logo \(x=-6\)
Logo, as raízes da equação são \(S=\{3,-6\}\).
d. \(x^{2}+2 x-35=0\)
Temos que:
\(x^{2}+2 x+1^{2}=35+1^{2}\)
logo,
\((x+1)^{2}=36\)
((x+1)^{2}=36\)
\(x+1=\pm \sqrt{36}\)
\(x+1=\pm 6\)
i) \(x+1=6\) logo \(x=5\)
ii) \(x+1=-6\) logo \(x=-7\)
e. \(x^{2}-6 x+5=0\)
Temos que:
\(x^{2}-6 x+3^{2}=-5+3^{2}\)
((x+3)^{2}=4)
\(x+3=\pm \sqrt{4}\)
\(x+3=\pm 2\)
Então,
i) \(x+3=2=x=-1\)
ii) \(x+3=-2=x=-5\)
Logo, as raízes da equação são \(S={-1,-5}\).
2. O estacionamento da empresa do Walter possui uma área de \(375 \mathrm{~m}^{2}\) e ele pretende aumentar a área para \(600 \mathrm{~m}^{2}\). A medida dos lados do atual terreno é de \(15 \mathrm{~m}\) por \(25 \mathrm{~m}\), conforme mostra a imagem abaixo.
Em quantos metros Walter deve aumentar nas dimensões do estacionamento para que a nova área seja 600 m², ou seja, qual o valor de y?
a. \(5 \mathrm{~m}\).
b. \(7 \mathrm{~m}\).
c. \(9 \mathrm{~m}\).
d. \(11 \mathrm{~m}\).
Resposta:
Calculamos a área de um retângulo fazendo o produto entre a base e a altura.
A = b.h
\((15+y)(25+y)-375=600\)
\(375+15 y+25 y+y^{2}=600\)
\(375+40 y+y^{2}=600\)
\(y^{2}+40 y+375-600=0\)
\(y^{2}+40 y-225=0\)
\(y^{2}+40 y-225=0 \)
\(y^{2}+40 y=225\)
Completando o quadrado temos:
\(y^{2}+40 y+20^{2}=225+20^{2}\)
\((y+20)^{2}=625\)
\((y+20)^{2}=625=y+20=\pm \sqrt{625}=y+20=\pm 25\)
O que nos dá:
i) \(y+20=25\) logo \(y=5\)
ii) \(y+20=-25\) logo \(y=-45\)
\(y=5\), soma-se \(15+y\) sendo \(y = 5\) temos \(15+5=20\) e \(25+5=30\)
3. (SARESP, 2012) Cortando quadradinhos de \(4 \mathrm{~cm}^{2}\) nos cantos de uma folha de cartolina quadrada e dobrando os lados, obtemos uma caixa com \(128 \mathrm{~m}^{3}\) de volume.
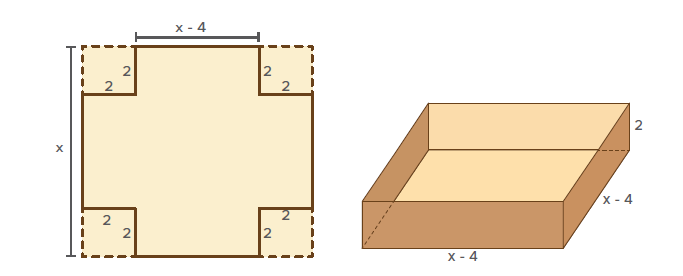
Determine as dimensões dessa caixa.
a. \(12 m, 12 m\) e \(2 m\).
b. \(10 \mathrm{~m}, 10 \mathrm{~m}\) e \(2 \mathrm{~m}\).
c. \(6 m, 6 m\) e \(2 m\).
d. \(8 m, 8 m\) e \(2 m\).
Resposta:
\((x-4)^{2} \cdot 2=128\)
\(\left(x^{2}-8 x+16\right) \cdot 2=128\)
\(2 x^{2}-16 x+32=128\)
\(2 x^{2}-16 x+32-128=0\)
\(2 x^{2}-16 x-96=0 \quad \quad(\div 2)\)
\(x^{2}-8 x-48=0 \)
\(x^{2}-8 x=48\)
Completando o quadrado temos:
\(x^{2}-8 x+4^{2}=48+4^{2}\)
\((x-4)^{2}=64\)
\(x-4=\pm \sqrt{64}\)
\(x-4=\pm 8\)
O que nos dá:
i) \(x-4=8\) logo \(x=12\)
ii) \(x-4=-8\) logo \(x=-4\)
Logo, considerando que \(x=12\), podemos achar a medida dos lados fazendo \(x-4\) temos \(12-4=8). Logo, as dimensões da caixa é \(8 m, 8 m\) e \(2 m\).
4. (AAP, 2017 – Adaptado) Um canteiro na forma de um quadrado foi reduzido de modo a ser contornado por uma calçada com \(2 \mathrm{~m}\) de largura, conforme a figura. Com isso, sua área passou a ser de \(144 \mathrm{~m}^{2}\).
A medida do lado que corresponde ao canteiro menor é:
a. \(6 \mathrm{~m}\).
b. \(8 \mathrm{~m}\).
c. \(12 \mathrm{~m}\).
d. \(16 \mathrm{~m}\).
Resposta:
A área do quadrado é dada pelo quadrado de um dos seus lados. Sendo assim,
(\mathrm{A}=\mathrm{l}^{2}) temos que ((x-4)(x-4)=144 \Rightarrow (x-4)^{2}=144).
Utilizando a técnica da fatoração do trinômio quadrado perfeito e resolvemos a equação.
((x-4)^{2}=144 \Rightarrow x-4=\pm \sqrt{144} \Rightarrow x-4=\pm 12) portanto (x=16) ou (x = -8). Substituindo em (x-4), que é a expressão algébrica que representa a medida do lado, (16-4=12). Logo, a medida do lado do canteiro menor é (12 \mathrm{~m}).
A alternativa correta é a letra c.
5. (AAP, 2017) Se o produto de dois fatores é zero, necessariamente um deles é igual a zero. Assim, as raizes reais da equação \((x+2) \cdot(x-6)=0\) são
a. \(2 e-6\).
b. \(-2\) e 6 .
c. \(2 e-2\).
d. 2 e 6.
Dada a equação: \((x+2) \cdot(x-6)=0\). Considerando a afirmação do enunciado têm-se que: \((x+2)=0\) ou \((x-6)=0\)
i) \(x=-2\)
ii) \(x=6\)
Logo, as raízes da equação estão no conjunto solução \(S=\{-2,6\}\).
A alternativa correta é a letra B.
6. Caro estudante, utilizando os significados que você desenvolveu até aqui sobre resolução de equações polinomial do \(2^{\circ}\) grau por meio de fatoração, elabore e apresente para o professor uma situação-problema cuja solução também seja por meio da fatoração de polinômios.
Was this helpful?
10 / 0